Часть математики, изучающая целые числа, называется арифметикой или теорией чисел. Это один из самых красивых разделов математики. Хотя школьники знакомятся с ним очень рано, он является довольно трудным. В арифметике имеется много задач, еще не решенных учеными, хотя их формулировку может понять даже первоклассник. О некоторых из них будет идти речь ниже.
Сначала опишем объекты, о которых пойдет речь.
1. Натуральные числа - это числа ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() , ... Они возникают в процессе счета и означают
количество предметов. Множество всех натуральных чисел
обозначается через
, ... Они возникают в процессе счета и означают
количество предметов. Множество всех натуральных чисел
обозначается через ![]()
![]() .
.
2. Целые числа - это числа ..., ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() , ..., т.е. число
, ..., т.е. число ![]()
![]() , натуральные числа и числа, противоположные
по знаку натуральным. Множество всех целых чисел обозначается
через
, натуральные числа и числа, противоположные
по знаку натуральным. Множество всех целых чисел обозначается
через ![]()
![]() . Натуральные числа можно складывать и умножать.
Вычитание натуральных чисел определяется как операция,
обратная сложению. А именно, равенство
. Натуральные числа можно складывать и умножать.
Вычитание натуральных чисел определяется как операция,
обратная сложению. А именно, равенство ![]()
![]() означает, что
означает, что ![]()
![]() . Это вычитание выполнимо не всегда, а лишь
в том случае, когда
. Это вычитание выполнимо не всегда, а лишь
в том случае, когда ![]()
![]() . В множестве целых чисел вычитание натуральных
чисел всегда выполнимо. А именно, надо положить
. В множестве целых чисел вычитание натуральных
чисел всегда выполнимо. А именно, надо положить ![]()
![]() , а если
, а если ![]()
![]() , то
, то ![]()
![]() . Сложение любых целых чисел и их вычитание, а
также умножение выполняются с помощью известных правил
знаков.
. Сложение любых целых чисел и их вычитание, а
также умножение выполняются с помощью известных правил
знаков.
3. Свойства арифметических операций хорошо известны. Они
часто используются без специального упоминания о них. Всюду в дальнейшем буквы
![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() означают любые целые числа.
означают любые целые числа.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Если ![]()
![]() , то
, то ![]()
![]() или
или ![]()
![]()
Следствие. Если ![]()
![]() ,
, ![]()
![]() и
и ![]()
![]() , то
, то ![]()
![]() , т.е. уравнение
, т.е. уравнение ![]()
![]() имеет не более одного решения в целых числах.
имеет не более одного решения в целых числах.
4. Делимость. Определение.
Пусть ![]()
![]() ,
, ![]()
![]() - целые числа. Говорят, что
- целые числа. Говорят, что ![]()
![]() - делитель
- делитель ![]()
![]() , или что
, или что ![]()
![]() делит
делит ![]()
![]() , или что
, или что ![]()
![]() кратно
кратно ![]()
![]() (
(![]()
![]() - кратное
- кратное ![]()
![]() ), или что
), или что ![]()
![]() делится на
делится на ![]()
![]() , если существует такое целое число
, если существует такое целое число ![]()
![]() , что
, что ![]()
![]() . Записывают этот факт в виде:
. Записывают этот факт в виде: ![]()
![]() .
.
Упражнение. Докажите, что
если ![]()
![]() и
и ![]()
![]() , то
, то ![]()
![]() и
и ![]()
![]() ;
;
если ![]()
![]() и
и ![]()
![]() - любое целое число, то
- любое целое число, то ![]()
![]() .
.
Проследите, какие из правил, приведенных в п. 3, здесь применяются.
5. Деление с остатком. Определение.
Пусть ![]()
![]() - целое,
- целое, ![]()
![]() - натуральное число. Разделить с остатком
- натуральное число. Разделить с остатком
![]()
![]() на
на ![]()
![]() - значит найти такие целые числа
- значит найти такие целые числа ![]()
![]() и
и ![]()
![]() , что
, что ![]()
![]() , где число
, где число ![]()
![]() таково, что
таково, что ![]()
![]() .
.
Число ![]()
![]() называется остатком, а число
называется остатком, а число ![]()
![]() - частным.
- частным.
Пример. Разделим с остатком ![]()
![]() на
на ![]()
![]() . Имеем:
. Имеем: ![]()
![]() . Отсюда остаток равен
. Отсюда остаток равен ![]()
![]() , а частное равно
, а частное равно ![]()
![]() .
.
Теорема 1. Пусть даны любые целое число
![]()
![]() и натуральное число
и натуральное число ![]()
![]() . Тогда разделить
. Тогда разделить ![]()
![]() на
на ![]()
![]() с остатком можно, и притом единственным образом
(т.е. числа
с остатком можно, и притом единственным образом
(т.е. числа ![]()
![]() и
и ![]()
![]() из определения деления с остатком существуют
и единственны).
из определения деления с остатком существуют
и единственны).
Доказательство. Для доказательства
существования чисел ![]()
![]() и
и ![]()
![]() надо фактически "измерить" отрезок длины
надо фактически "измерить" отрезок длины
![]()
![]() , приняв за единицу измерения отрезок длины
, приняв за единицу измерения отрезок длины
![]()
![]() . Если
. Если ![]()
![]() , т.е.
, т.е. ![]()
![]() - натуральное, то надо отложить внутри
отрезка длины
- натуральное, то надо отложить внутри
отрезка длины ![]()
![]() отрезок длины
отрезок длины ![]()
![]() столько раз, чтобы остаток
столько раз, чтобы остаток ![]()
![]() оказался меньше
оказался меньше ![]()
![]() , так что еще раз
, так что еще раз ![]()
![]() отложить уже нельзя. Тогда
отложить уже нельзя. Тогда ![]()
![]() - число уложившихся отрезков длины
- число уложившихся отрезков длины ![]()
![]() . Если
. Если ![]()
![]() , то надо взять
, то надо взять ![]()
![]() . Если
. Если ![]()
![]() , то надо сделать то же самое, но откладывать
отрезки длины
, то надо сделать то же самое, но откладывать
отрезки длины ![]()
![]() в левую сторону и дождаться, пока конец очередного
отрезка попадет в первый раз левее левого конца отрезка,
изображающего
в левую сторону и дождаться, пока конец очередного
отрезка попадет в первый раз левее левого конца отрезка,
изображающего ![]()
![]() , или точно в его конец.
, или точно в его конец.
Доказательство единственности можно получить из этой же картинки, а можно
провести методом от противного, что мы сейчас и сделаем. Пусть ![]()
![]() разделено на
разделено на ![]()
![]() двумя способами:
двумя способами:
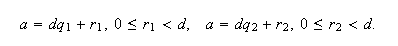 Вычитая второе равенство из первого, получим:
Вычитая второе равенство из первого, получим:
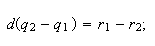 имеем, очевидно,
имеем, очевидно, ![]()
![]() , но в интервале
, но в интервале ![]()
![]() лишь число
лишь число ![]()
![]() является целым кратным числа
является целым кратным числа ![]()
![]() . Поэтому
. Поэтому ![]()
![]() и
и ![]()
![]() , что и требовалось доказать.
, что и требовалось доказать.
Замечание. Фактически частное и остаток от деления
натурального числа ![]()
![]() на натуральное число
на натуральное число ![]()
![]() находятся по известному способу деления "уголком".
находятся по известному способу деления "уголком".
6. Простые числа. Натуральное число ![]()
![]() называется простым, если его натуральными
делителями являются только числа
называется простым, если его натуральными
делителями являются только числа ![]()
![]() и
и ![]()
![]() . Примеры:
. Примеры: ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() - простые числа. Число
- простые числа. Число ![]()
![]() удобно не считать простым числом.
удобно не считать простым числом.
7. Наибольший общий делитель (НОД) двух
целых чисел ![]()
![]() и
и ![]()
![]() , не равных одновременно нулю, - это наибольшее
натуральное число
, не равных одновременно нулю, - это наибольшее
натуральное число ![]()
![]() , являющееся одновременно делителем для
, являющееся одновременно делителем для ![]()
![]() и для
и для ![]()
![]() , т.е.
, т.е. ![]()
![]() и
и ![]()
![]() . Мы будем обозначать НОД чисел
. Мы будем обозначать НОД чисел ![]()
![]() и
и ![]()
![]() через
через ![]()
![]() . Ясно, что НОД существует, поскольку делитель
числа
. Ясно, что НОД существует, поскольку делитель
числа ![]()
![]() при
при ![]()
![]() не может быть больше, чем
не может быть больше, чем ![]()
![]() , где
, где ![]()
![]() - абсолютная величина (или модуль) числа
- абсолютная величина (или модуль) числа
![]()
![]() .
.
8. Алгоритм Евклида. Вообще алгоритмом называется способ
достижения какой-либо цели, описанный так четко, что его может осуществить
машина. Алгоритм Евклида - это способ нахождения НОД двух натуральных чисел
![]()
![]() и
и ![]()
![]() .
.
Предположим для определенности, что ![]()
![]() . Разделим
. Разделим ![]()
![]() на
на ![]()
![]() с остатком:
с остатком:

Теперь имеется две возможности:
1) ![]()
![]() . Тогда ясно, что
. Тогда ясно, что ![]()
![]() .
.
2) ![]()
![]() . Тогда нужно воспользоваться следующим замечательным
соотношением:
. Тогда нужно воспользоваться следующим замечательным
соотношением:
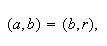 вытекающим из того, что каждый общий делитель
вытекающим из того, что каждый общий делитель ![]()
![]() и
и ![]()
![]() делит
делит ![]()
![]() и каждый общий делитель
и каждый общий делитель ![]()
![]() и
и ![]()
![]() делит
делит ![]()
![]() (это видно из определения деления с остатком),
так что множество общих делителей
(это видно из определения деления с остатком),
так что множество общих делителей ![]()
![]() и
и ![]()
![]() совпадает с множеством общих делителей
совпадает с множеством общих делителей ![]()
![]() и
и ![]()
![]() , в частности, совпадают наибольшие общие делители.
Имеем:
, в частности, совпадают наибольшие общие делители.
Имеем:
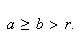 Теперь вместо
Теперь вместо ![]()
![]() надо находить
надо находить ![]()
![]() . Деля
. Деля ![]()
![]() на
на ![]()
![]() и обозначая остаток через
и обозначая остаток через ![]()
![]() , мы получаем:
, мы получаем:
 Если
Если ![]()
![]() , то
, то ![]()
![]() . Если же
. Если же ![]()
![]() , то надо делить
, то надо делить ![]()
![]() на
на ![]()
![]() и так далее, пока не получится остаток, равный
и так далее, пока не получится остаток, равный
![]()
![]() . В конце концов это произойдет, поскольку
остатки все время уменьшаются. Последний отличный от нуля
остаток и будет равен
. В конце концов это произойдет, поскольку
остатки все время уменьшаются. Последний отличный от нуля
остаток и будет равен ![]()
![]() . Окончательно запишем весь процесс так:
. Окончательно запишем весь процесс так:
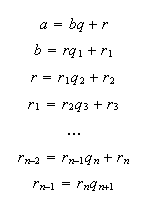
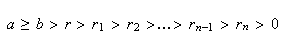 Тогда
Тогда ![]()
![]() .
.
Пример. Вычислим ![]()
![]() . Деля число
. Деля число ![]()
![]() на число
на число ![]()
![]() с остатком, получим
с остатком, получим
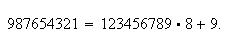 Число
Число ![]()
![]() делится на
делится на ![]()
![]() . Поэтому
. Поэтому ![]()
![]() .
.