Лекция 2. Выражение НОД двух чисел через эти числа.
Основная теорема арифметики

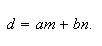
Теорема 2. Пусть $d=(a,b)$. Тогда существуют такие целые числа $m$ и $n$, что
MATH

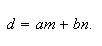
Доказательство. Зафиксируем целые числа $a$ и $b$ и рассмотрим множество $I$ всех целых чисел, представимых в виде $am+bn$, где $m$ и $n$ - целые. Ясно, что $a$ и $b$ принадлежат множеству $I$ (например, $a=a\cdot1+b\cdot0$). Далее, если $s$ и $t$ принадлежат $I$, а $q_1$ и $q_2$ - целые, то число $q_1s+q_2t$ принадлежит $I$, поскольку если $s=am_1+bn_1$, $t=am_2+bn_2$, где $m_1$, $n_1$, $m_2$, $n_2$ - целые числа, то MATH, а числа $q_1m_1+q_2m_2$ и $q_1n_1+q_2n_2$ - целые.

Рассмотрим теперь цепочку остатков из алгоритма Евклида. Пусть $a\ge b>0$. Делим $a$ на $b$: $a=bq+r$, $0\le r<b$. Так как $a$ и $b$ принадлежат $I$, то $r=a-bq$ тоже принадлежит $I$. Далее, если $r>0$, то надо делить $b$ на $r$: $b=rq_1+r_1$. Поскольку $b$ и $r$ принадлежат $I$, то $r_1=b-rq_1$ тоже принадлежит $I$. Рассуждая аналогично, мы видим, что все возникающие остатки принадлежат $I$, то есть представимы в виде $am+bn$, где $m$ и $n$ - целые. Поэтому последний ненулевой остаток, равный $d=(a,b)$, тоже принадлежит $I$, то есть представим в виде $am+bn$, что и требовалось доказать.

Следствие. Если $p\mid a$ и $p\mid b$, то $p\mid (a,b)$.

Теорема 3. Пусть $a$, $b$ и $n$ - целые числа, причем числа $a$ и $b$ не равны одновременно нулю. Пусть $d=(a,b)$. Уравнение $ax+by=n$ разрешимо в целых числах тогда и только тогда, когда $d\mid n$.

Доказательство. Если уравнение имеет целочисленное решение $x$, $y$, то из $d\mid a$, $d\mid b$ вытекает, что $d\mid n$ в силу самого уравнения. Обратно, если $d\mid n$, то $n=dm$, где $m$ - целое, и записав $d$ в виде $d=as+bt$, где $s$ и $t$ - целые числа, мы получим, что $n=dm=a(sm)+b(tm)$, то есть уравнение имеет решение $x=sm$, $y=tm$. Теорема доказана.

Определение. Целые числа $a$ и $b$ называются взаимно простыми, если $(a,b)=1$.

Теорема 4. Если $a$, $b$ и $c$ - целые числа, $a\mid bc$ и $(a,b)=1$, то $a\mid c$.

Доказательство. Найдем такие целые числа $x$ и $y$, что $ax+by=1$. Отсюда $acx+bcy=c$. Но $a\mid acx$ и $a\mid bcy$, так как $a\mid bc$. Поэтому $a\mid c$, что и требовалось доказать.

Следствие 1. Если $a$ и $b$ - целые числа, $p$ - простое число и $p\mid ab$, то $p\mid a$ или $p\mid b$.

Доказательство. Ясно, что $(p,a)$ может быть равен либо $1$, либо $p$. Если $(p,a)=p$, то $p\mid a$, если же $(p,a)=1$, то $p\mid b$ по теореме 4.

Следствие 2. Если $p$ - простое, MATH, где каждое $p_i$ простое, то $p$ совпадает с одним из $p_i$.

Доказательство. Имеем: MATH. Поэтому либо $p\mid p_r$ (а тогда $p=p_r$), либо MATH. Далее, в последнем случае либо $p=p_{r-1}$, либо MATH и т. д. В конце концов получаем, что $p$ совпадает с одним из $p_i$.

Теорема 5 (Основная теорема арифметики). Любое натуральное число, большее $1$, единственным образом разлагается на простые множители.

Доказательство. 1. Докажем существование разложения, то есть представления числа $n\ge 2$ в виде $n=p_1p_2\ldots p_s$, где $p_i$ - простые числа. Возьмем наименьший отличный от $1$ натуральный делитель $p_1$ числа $n$. Ясно, что $p_1$ - простое число, так как если бы $p_1$ имело натуральные делители, не равные $1$ и $p_1$, то эти делители были бы еще меньшими делителями $n$. Если $p_1=n$, то разложение $n$ закончено. Если $p_1\ne n$, то $n=p_1n_1$, где $n_1<n$. Возьмем теперь в качестве $p_2$ наименьший отличный от $1$ натуральный делитель числа $n_1$ и т. д.

2. Докажем единственность разложения. Пусть MATH - два разложения числа $n$ на простые множители. В силу следствия 2 из предыдущей теоремы $p_1$ совпадает с одним из $q_i$. Сократим на $p_1$ и проведем то же самое рассуждение. В результате получается, что выписанные разложения числа $n$ отличаются лишь порядком сомножителей. Теорема доказана.