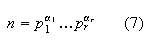 где
где
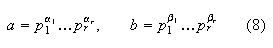 с одними и
теми же
простыми
с одними и
теми же
простыми
При
разложении
на простые
множители
числа n
удобно
объединять
одинаковые
сомножители,
запиывая их
в виде
степеней.
Так как
любое число
натуральное
число
![]()
![]() можно
записать в
виде
можно
записать в
виде
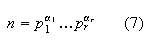 где
где
![]()
![]() - простые
числа,
- простые
числа,
![]()
![]() ,
,
![]()
![]() .
В этой
записи можно
было бы
считать, что
.
В этой
записи можно
было бы
считать, что
![]()
![]() (то есть
(то есть
![]()
![]() ),
однако
удобно
разрешать и
),
однако
удобно
разрешать и
![]()
![]() .
Тогда
некоторые
сомножители
равны
.
Тогда
некоторые
сомножители
равны
![]()
![]() и
соответствующее
число
и
соответствующее
число
![]()
![]() в разложении
(7) фактически
отсутствует.
Благодаря
этому мы
можем любые
два числа
в разложении
(7) фактически
отсутствует.
Благодаря
этому мы
можем любые
два числа
![]()
![]() записать в
виде:
записать в
виде:
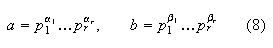 с одними и
теми же
простыми
с одними и
теми же
простыми
![]()
![]() ,
...,
,
...,
![]()
![]() .
Здесь
.
Здесь
![]()
![]() ,
,
![]()
![]() -
неотрицательные
целые числа.
-
неотрицательные
целые числа.
Теорема 6.
Если
![]()
![]() и
и
![]()
![]() записаны в
виде (8), то
записаны в
виде (8), то
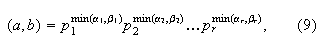 где
где
![]()
![]() означает
наименьшее
из двух
чисел
означает
наименьшее
из двух
чисел
![]()
![]() и
и
![]()
![]() .
.
Доказательство.
Если
![]()
![]() ,
то
разложение
,
то
разложение
![]()
![]() на простые
множители по
теореме
единственности
есть часть
разложения
на простые
множители по
теореме
единственности
есть часть
разложения
![]()
![]() (если
(если
![]()
![]() ,
то
разложение
,
то
разложение
![]()
![]() можно
получить,
перемножая
разложения
можно
получить,
перемножая
разложения
![]()
![]() и
и
![]()
![]() ).
Поэтому
).
Поэтому
![]()
![]() ,
где
,
где
![]()
![]() .
Если к тому
же
.
Если к тому
же
![]()
![]() ,
то
,
то
![]()
![]() ,
откуда
,
откуда
![]()
![]() .
НОД
получается
при
.
НОД
получается
при
![]()
![]() .
Теорема
доказана.
.
Теорема
доказана.
Пример.
Рассмотрим
числа
![]()
![]() и
и
![]()
![]() .
Имеем:
.
Имеем:
![]()
![]() ,
,
![]()
![]() .
Отсюда
.
Отсюда
![]()
![]() .
.
Определение.
Наименьшим
общим
кратным (НОК)
двух
отличных от
![]()
![]() целых чисел
целых чисел
![]()
![]() и
и
![]()
![]() называется
наименьшее
число
называется
наименьшее
число
![]()
![]() ,
для которого
,
для которого
![]()
![]() и
и
![]()
![]() .
НОК чисел
.
НОК чисел
![]()
![]() и
и
![]()
![]() мы будем
обозначать
через
мы будем
обозначать
через
![]()
![]() .
.
Теорема 7.
Пусть
натуральные
числа
![]()
![]() и
и
![]()
![]() записаны в
виде (8). Тогда:
записаны в
виде (8). Тогда:
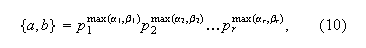 где
где
![]()
![]() означает
наибольшее
из двух
чисел
означает
наибольшее
из двух
чисел
![]()
![]() ,
,
![]()
![]() .
.
Доказательство аналогично доказательству предыдущей теоремы.
Пример.
![]()
![]() .
.
Следствие
1.
![]()
![]() .
.
В самом деле,
![]()
![]() .
.
Следствие
2. Если
![]()
![]() и
и
![]()
![]() ,
то
,
то
![]()
![]()
![]()
![]()
![]()
![]() .
.
Теорема 8 (Евклид). Простых чисел бесконечно много.